로봇 위치 추적 정확도 개선: 가속도 피드포워드 최적화 여정

기존 수치 미분 방식의 가속도 피드포워드(FF)로는 약 5% 개선에 그쳤습니다. 이론적으로 기대한 것보다 훨씬 낮은 수치입니다.

핵심 질문: "모션 플래너의 가속도를 직접 사용하면 얼마나 더 좋아질까?"

이 질문에 답하기 위해 6가지 가속도 획득 방법을 체계적으로 비교했습니다.

결론 먼저

방법	Position RMSE	개선율	Torque RMSE
A0 (없음)	0.001389 rad	기준	2.77 Nm
A1 (수치 미분)	0.001141 rad	+17.8%	4.29 Nm (+55%)
A4 (LPF)	0.001095 rad	+21.2%	2.68 Nm (-3%)

최적 방법: 플래너 가속도 + Low-Pass Filter (alpha=0.3)

• 위치 정확도 21.2% 개선
• 토크 변동 3% 감소 (기준선 대비)

시스템 아키텍처

핵심 발견: ROS2 JointTrajectoryController가 이미 Quintic Spline 보간으로 가속도를 계산하고 있었습니다. 별도 수치 미분이 필요 없습니다.

새로운 문제: Quintic Spline은 위치/속도/가속도의 연속성을 보장하지만, Jerk(가속도의 미분)는 불연속입니다. 웨이포인트 경계에서 고주파 성분이 발생하여 기계적 진동을 유발할 수 있습니다.

로봇 동역학 방정식

$$\tau = M(q)\ddot{q} + C(q, \dot{q})\dot{q} + g(q) + \tau_{friction}$$

항	설명	FF와의 관계
$M(q)\ddot{q}$	관성 토크	가속도 FF 대상
$C(q, \dot{q})\dot{q}$	코리올리/원심력 토크	-
$g(q)$	중력 보상 토크	-
$\tau_{friction}$	마찰 보상 토크	-

6가지 가속도 획득 방법 비교

코드	방법	설명
A0	None	가속도 FF 없음 (기준선)
A1	NumDiff	속도 명령의 수치 미분 (기존 방식)
A2	ABG	Alpha-Beta-Gamma 필터
A3	Planner	JTC 가속도 직접 사용 (필터 없음)
A4	LPF	JTC 가속도 + Low-Pass Filter
A5	JerkLimit	JTC 가속도 + Jerk 제한

수치 미분 (A1)의 문제

acceleration[k] = (velocity[k] - velocity[k-1]) / dt;

문제	원인	결과
위상 지연	이산 미분은 현재와 과거 샘플만 사용	실제 가속도보다 지연된 값 출력
노이즈 증폭	미분 연산이 고주파 성분을 증폭	토크 변동 55% 증가

Low-Pass Filter (A4)

플래너 가속도를 직접 사용하면(A3) 웨이포인트 경계에서 Jerk 불연속이 발생합니다. LPF는 이 고주파 성분을 제거하여 부드러운 가속도 신호를 만듭니다.

y[k] = alpha * x[k] + (1 - alpha) * y[k-1];

즉, 새 출력 = (alpha × 새 입력) + ((1-alpha) × 이전 출력) 입니다.

변수	의미
x[k]	새로 들어온 가속도 값
y[k-1]	이전 필터 출력
alpha	새 값 반영 비율 (0~1)

alpha=0.3이면 새 값 30% + 이전 값 70%로, 급격한 변화가 완화됩니다.

alpha와 차단 주파수의 관계 ($f_s$ = 샘플링 주파수 1kHz, $f_c$ = 차단 주파수):

$$f_c \approx \frac{\alpha \cdot f_s}{2\pi}$$

$f_c$ 이하 주파수는 통과하고, 이상은 감쇠됩니다.

Alpha	차단 주파수	특성
0.1	~16 Hz	과도한 필터링, 응답 지연
0.2	~32 Hz	안정적, 약간의 응답 지연
0.3	~48 Hz	최적 균형점
0.5	~80 Hz	빠른 응답, 토크 증가 시작
0.7	~112 Hz	필터링 약함, 토크 11% 증가

실험 결과

1차 실험: 6가지 방법 비교

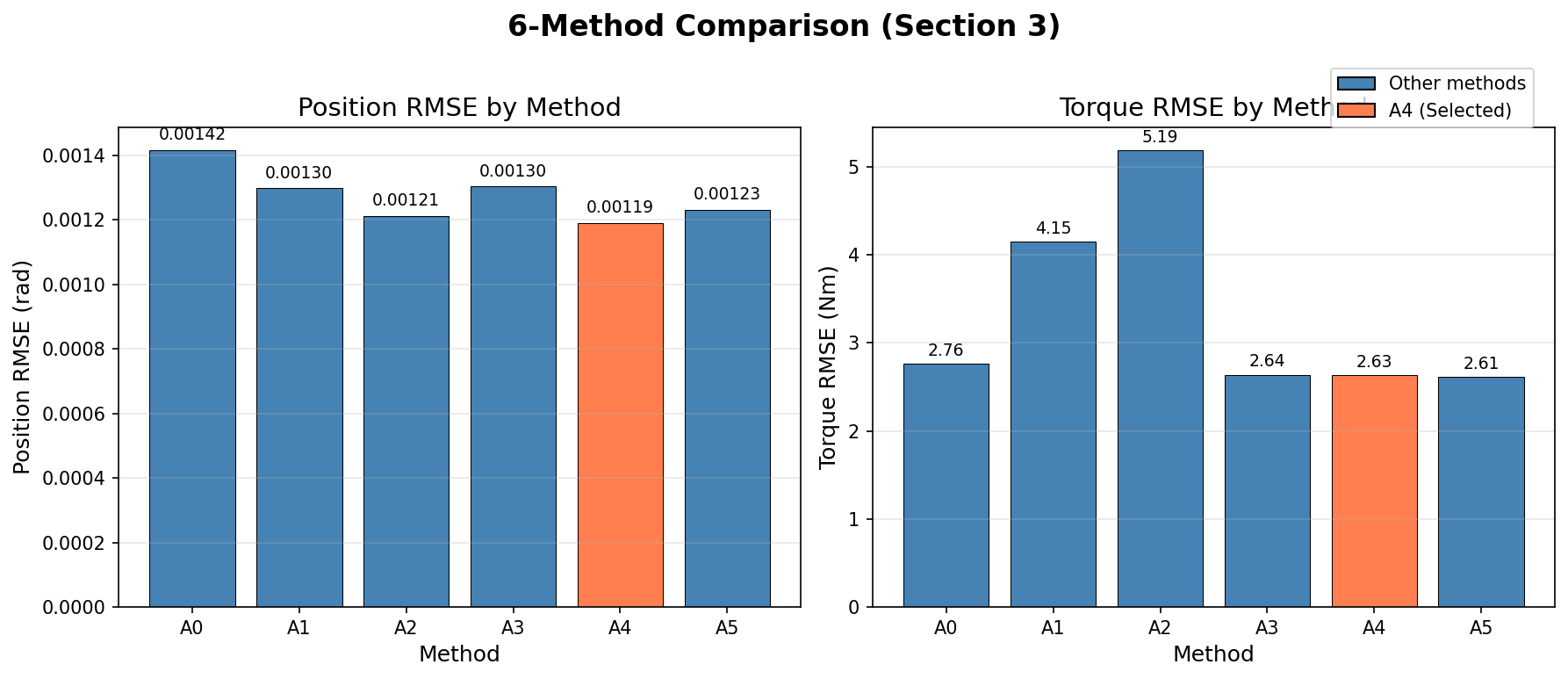
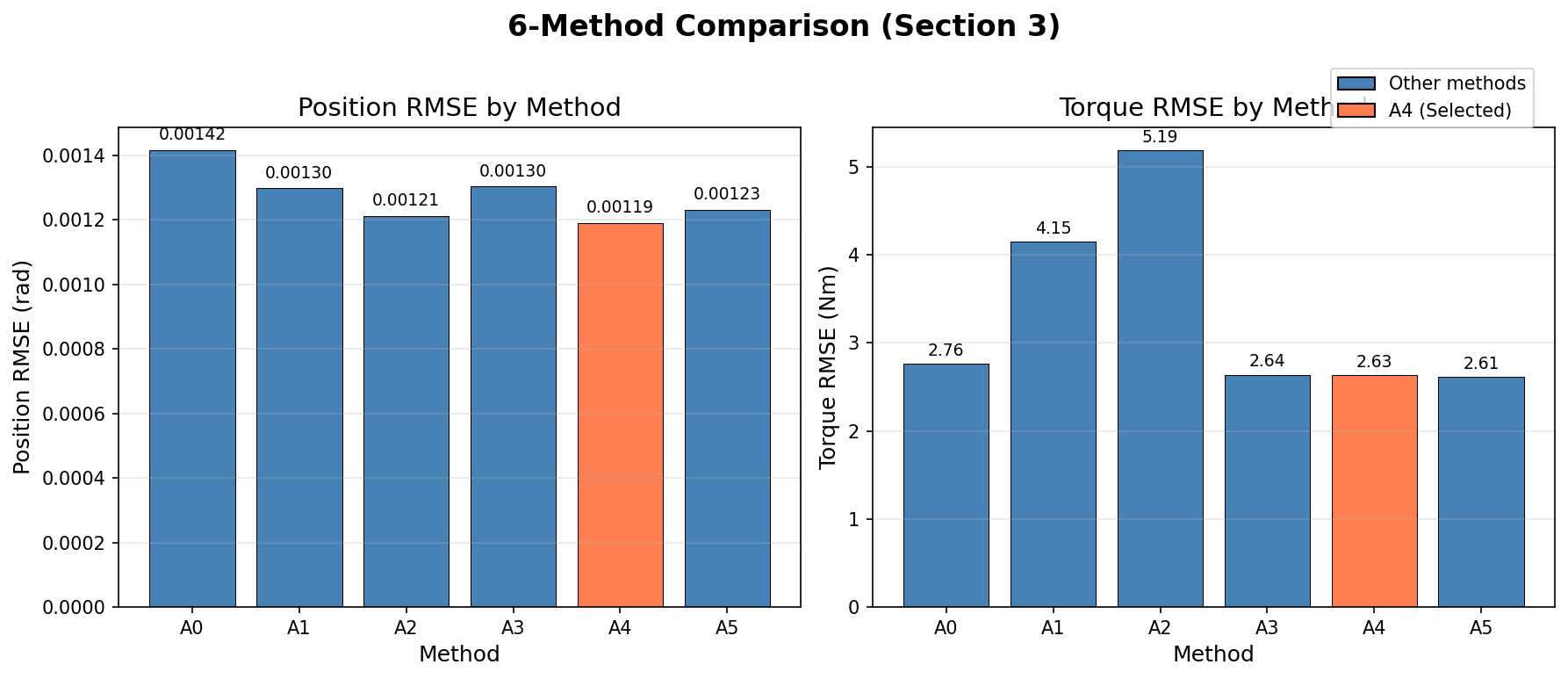
Position RMSE(좌)와 Torque RMSE(우) 비교. A4(LPF)가 최적 균형점

Position RMSE 순위:

순위	방법	RMSE (rad)	개선율
1	A4 (LPF)	0.001190	+16.0%
2	A2 (ABG)	0.001212	+14.4%
3	A5 (Jerk)	0.001231	+13.1%
4	A1 (NumDiff)	0.001297	+8.4%
5	A3 (Planner)	0.001302	+8.1%
6	A0 (None)	0.001416	기준

Torque RMSE:

방법	Torque RMSE	평가
A5 (Jerk)	2.61 Nm	안정
A4 (LPF)	2.63 Nm	안정
A3 (Planner)	2.64 Nm	안정
A0 (None)	2.76 Nm	기준
A1 (NumDiff)	4.15 Nm	+50% (경고)
A2 (ABG)	5.19 Nm	+88% (탈락)

A2(ABG) 탈락 이유: 위치는 좋지만 토크 변동이 너무 큽니다.

2차 실험: LPF 파라미터 튜닝

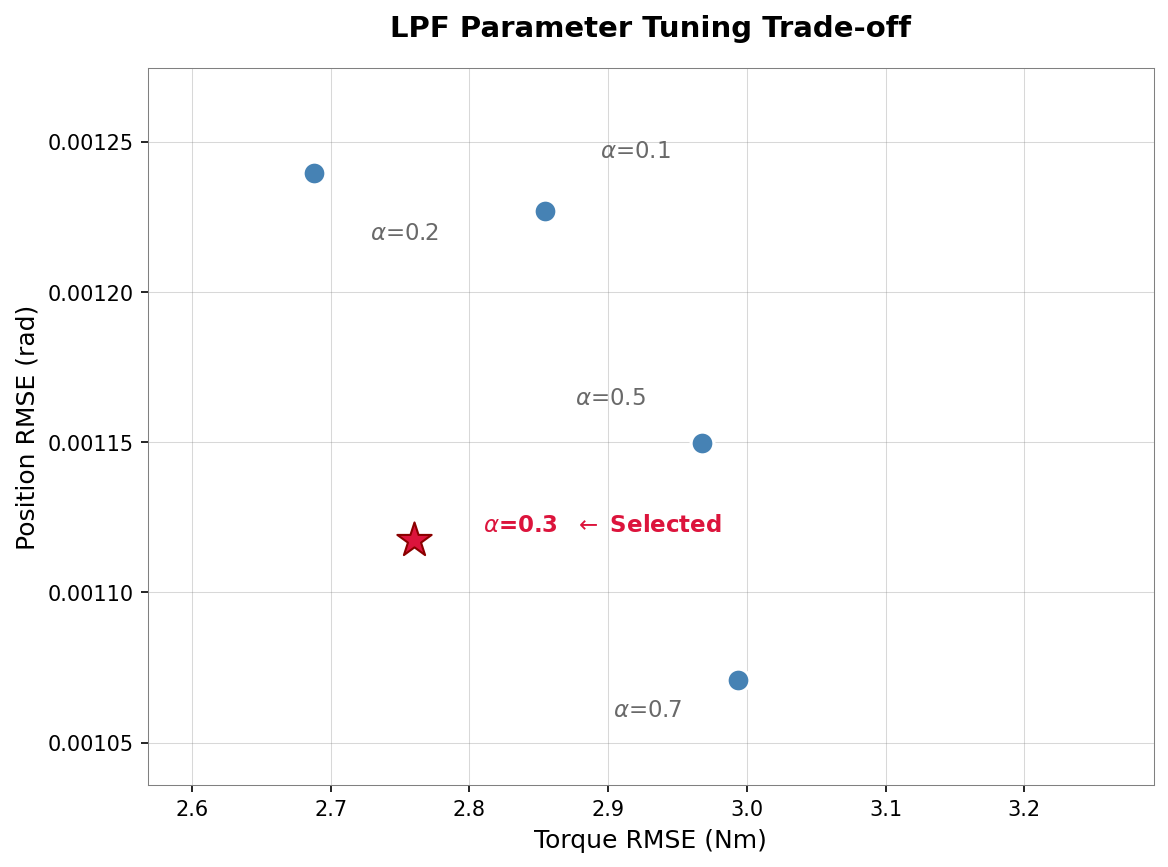
alpha 값에 따른 Position RMSE vs Torque RMSE 트레이드오프. alpha=0.3 선택

Alpha	차단 주파수	Position RMSE	vs alpha=0.2	Torque RMSE
0.1	~16 Hz	0.001227 rad	+1.0%	2.85 Nm
0.2	~32 Hz	0.001240 rad	기준	2.69 Nm
0.3	~48 Hz	0.001118 rad	-9.8%	2.76 Nm
0.5	~80 Hz	0.001150 rad	-7.3%	2.97 Nm
0.7	~112 Hz	0.001071 rad	-13.6%	2.99 Nm

alpha=0.3 선택 이유:

• Position 개선: alpha=0.2 대비 9.8% 개선
• Torque 안정: 기준선(2.77 Nm)과 거의 동일한 2.76 Nm
• 안전 마진: alpha=0.7은 토크 11.2% 증가

3차 실험: 최종 벤치마크

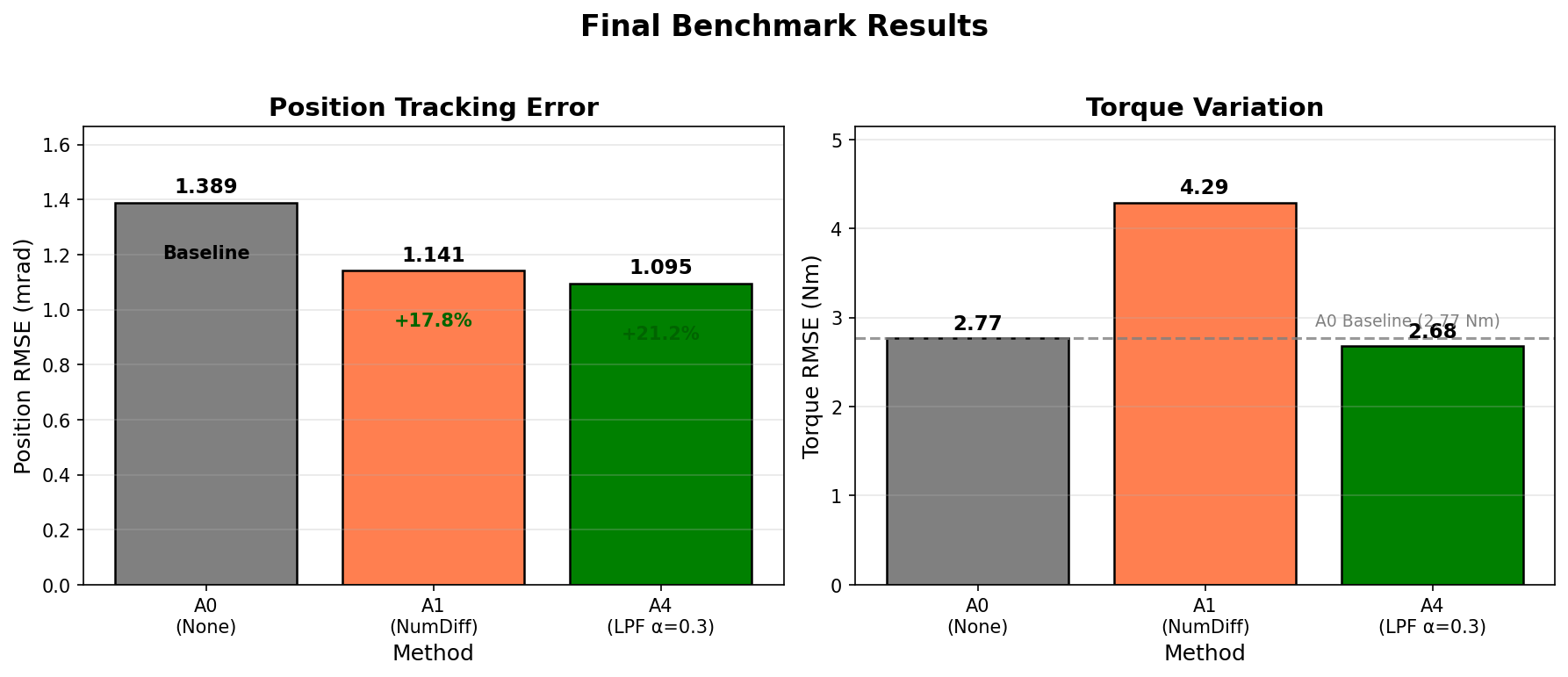
A0(기준), A1(수치 미분), A4(LPF) 최종 비교

Position 추적 성능:

방법	Position RMSE	표준편차	개선율
A4 (LPF)	0.001095 rad	0.000087	+21.2%
A1 (NumDiff)	0.001141 rad	0.000064	+17.8%
A0 (None)	0.001389 rad	0.000071	기준

Torque 안정성:

방법	Torque RMSE	표준편차	평가
A4 (LPF)	2.68 Nm	0.37	안정 (-3%)
A0 (None)	2.77 Nm	0.52	기준
A1 (NumDiff)	4.29 Nm	1.04	불안정 (+55%)

왜 플래너 가속도 단독(A3)으로는 부족한가?

플래너 가속도를 필터 없이 직접 사용하면 8.1% 개선에 그칩니다 (A4의 절반).

원인: 웨이포인트 경계에서 Jerk 불연속이 고주파 성분을 생성하여 컨트롤러에 부담을 줍니다.

왜 LPF(A4)가 Jerk Limiting(A5)보다 좋은가?

측면	LPF	Jerk Limiting
응답 특성	지수적 감쇠	선형 램프
수렴 속도	초기 빠른 응답, 점진적 수렴	일정 속도 접근, 느린 수렴
예시: Δacc=20 rad/s², MAX_JERK=50 rad/s³	빠름	400ms 소요

웜업 효과

실험 중 웜업 효과를 발견했습니다:

조건	웜업 전	웜업 후	차이
A3 (Planner)	0.001532 rad	0.001302 rad	15% 개선

시사점: 콜드 스타트 시 성능이 15% 저하될 수 있습니다. 실제 로봇 운영에서 고려해야 합니다.

실험 조건

파라미터	값	이유
테스트 관절	J1 (어깨)	최대 마찰(Fc=35Nm)로 FF 효과 극대화
속도 스케일	0.3, 0.4, 0.5	고속 조건에서 차이 명확화
가속도 스케일	0.5	고가속 조건
반복 횟수	속도당 4회	방향 균형 (정방향 2회 + 역방향 2회)
궤적	±30도 토글	표준 테스트 모션

핵심 정리

1. 기존 수치 미분(A1)의 한계: 이산 미분의 위상 지연과 노이즈 증폭으로 토크 변동이 55% 증가합니다.

2. ROS2 JTC가 이미 가속도를 계산합니다. 별도 수치 미분 없이 플래너 가속도를 직접 활용할 수 있습니다.

3. Jerk 불연속 문제: 플래너 가속도를 필터 없이 사용하면 웨이포인트 경계의 고주파 성분이 성능을 저하시킵니다.

4. 최적 방법: LPF (alpha=0.3)

   • Position RMSE: 21.2% 개선
   • Torque RMSE: 3% 감소
   • 위치 정확도와 토크 안정성을 동시에 개선

5. 웜업 효과: 콜드 스타트 시 15% 성능 저하가 발생할 수 있습니다.

단순한 1차 Low-Pass Filter가 위치 정확도와 토크 안정성을 동시에 개선하는 최적 해법이었습니다.