로봇이 3D 공간을 이해하는 방법: Voxel과 SDF

2D 이미지에서 가장 작은 단위는 픽셀(Pixel)입니다. 그렇다면 3D 공간의 픽셀은 무엇일까요? 바로 복셀(Voxel)입니다. Volume과 Pixel의 합성어로, 1×1×1 크기의 정육면체가 3D 공간을 채웁니다.

이 글에서는 로봇이 환경을 이해하기 위해 사용하는 Voxel, SDF(Signed Distance Fields), 그리고 그 변형인 TSDF와 ESDF를 설명합니다.

Voxel: 3D 공간의 데이터 컨테이너

Voxel은 직교 좌표계에서 고유한 3D 좌표 $(x, y, z)$ 를 가지는 데이터 컨테이너입니다. 각 Voxel에는 해당 위치의 물리적 속성을 저장할 수 있습니다:

색상 (RGB)
밀도
점유 여부 (Occupied/Free/Unknown)
장애물까지의 거리

Point Cloud vs Voxel

LiDAR나 깊이 카메라에서 얻는 Point Cloud와 Voxel은 근본적으로 다릅니다:

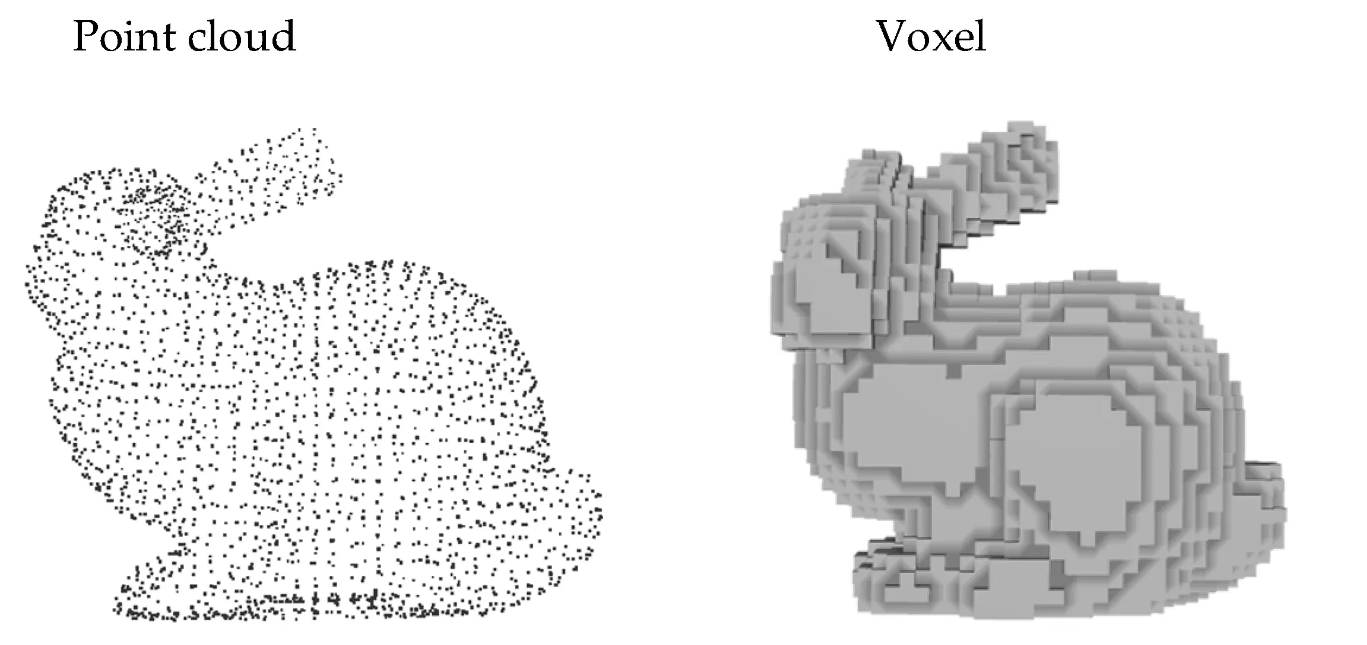
Point Cloud와 Voxel 비교

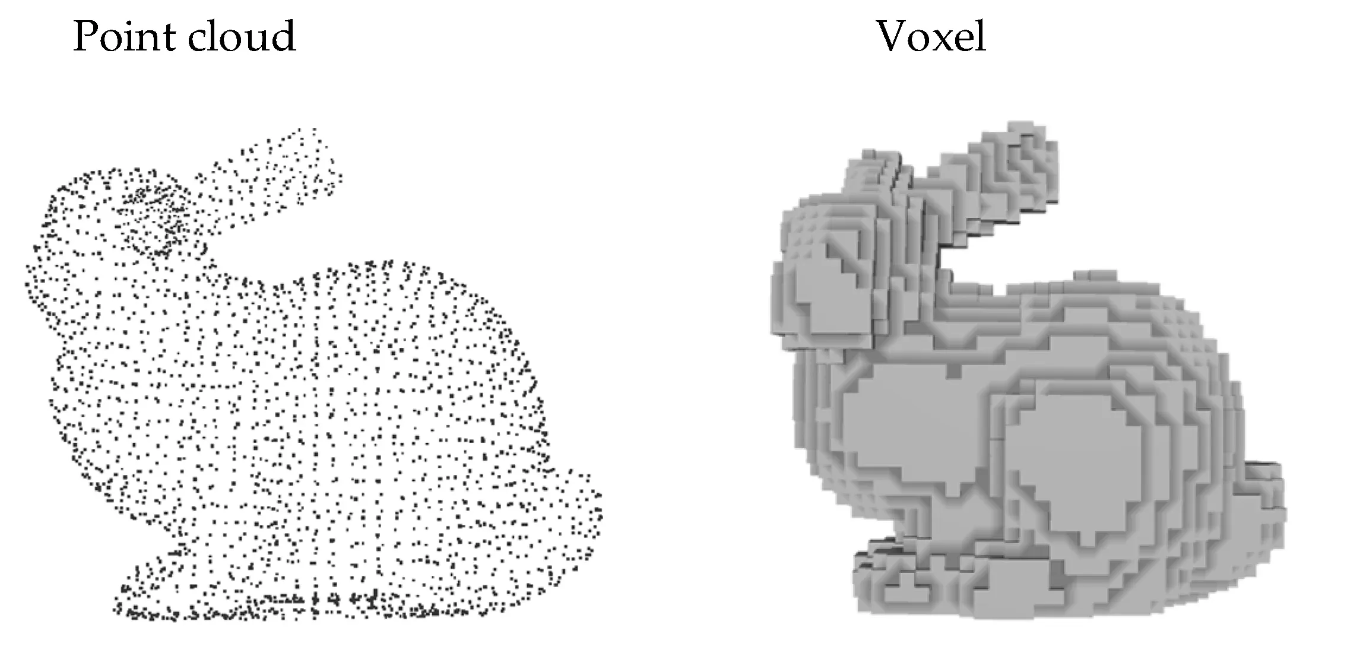
Stanford Bunny 모델의 Point Cloud(좌)와 Voxel(우) 표현 비교

측면	Point Cloud	Voxel
표현 방식	표면(Shell) - 센서에서 반사된 점들의 집합	부피(Volume) - 표면, 내부, 빈 공간 포함
좌표계	카메라 기준 (센서마다 다름)	고정된 공간 그리드, 고유 좌표
데이터 지속성	매 프레임 새 점 생성, 좌표 변환 및 중복 제거 필요	고정된 고유 좌표, 데이터 병합 용이
빈 공간 정보	없음	있음 (Occupancy Grid)

핵심 차이: Point Cloud는 "어디에 물체가 있는가"만 알려주지만, Voxel은 "어디가 비어있는가"도 알려줍니다.

Occupancy Grid Map

Voxel에 점유 정보(Occupancy)를 저장하면 3D 지도가 됩니다:

상태	의미
Occupied	장애물 존재
Free	빈 공간
Unknown	아직 탐색되지 않음

값은 0/1 이진값 또는 확률값으로 저장할 수 있습니다.

Occupancy Grid의 한계

단순 점유 정보만으로는 두 가지 문제를 해결할 수 없습니다:

문제 1: 안전 거리 검증

로봇은 부피를 가진 강체입니다. 현재 위치가 장애물에 얼마나 가까운지 알아야 안전한 이동이 가능합니다.

Occupancy Grid: 현재 위치가 Occupied인지만 확인 가능
한계: "얼마나 가까운가?"를 알 수 없음 → 매번 주변 Voxel을 탐색해야 함

문제 2: 경로 최적화를 위한 기울기 정보

현대 경로 계획 알고리즘은 부드러운 궤적 생성을 위해 기울기(Gradient) 정보가 필요합니다.

Occupancy Grid: 0/1 이산값 → 미분 불가능
한계: 최적화 기반 경로 계획에 사용 불가

SDF: Signed Distance Fields

SDF는 각 Voxel에 가장 가까운 장애물 표면까지의 거리를 미리 계산해서 저장합니다.

SDF의 구성 요소

값(거리): 가장 가까운 장애물까지의 유클리드 거리
부호:
- 양수(+): 장애물 외부
- 음수(−): 장애물 내부

SDF가 해결하는 문제

안전 거리 검증:

현재 위치의 SDF 값 = 3.5cm
→ 가장 가까운 장애물이 3.5cm 떨어져 있음
→ 로봇 반경이 3cm면 안전

주변 Voxel을 탐색할 필요 없이 단일 조회로 안전 거리를 확인할 수 있습니다.

기울기 기반 최적화:

SDF는 연속적인 거리값이므로 기울기(미분값)를 계산할 수 있습니다. 이를 통해:

장애물에서 멀어지는 방향을 알 수 있음
최적화 기반 경로 계획 알고리즘에 활용 가능

TSDF: Truncated SDF

TSDF는 일정 범위 이상의 거리값을 잘라낸(Truncate) SDF입니다.

TSDF의 특징

예시: Truncation 범위가 30cm인 경우
- 장애물 표면에서 30cm 이내: 정확한 거리값 저장
- 30cm 이상: "최대값(먼 곳)"으로 저장

TSDF의 장점

장점	설명
노이즈 제거	먼 거리의 부정확한 데이터 무시
부드러운 표면	여러 프레임을 누적하여 평균화
효율적 저장	표면 근처 데이터만 정밀하게 저장

TSDF 활용 사례

TSDF로 재구성한 Isaac Sim 환경

TSDF를 사용하여 Isaac Sim에 사무실 환경을 재건한 결과

주요 용도:

3D 표면 재구성 (Surface Reconstruction)
센서 노이즈 필터링
3D 환경 메시 생성

ESDF: Euclidean SDF

ESDF는 모든 Voxel에 대해 전체 유클리드 거리를 계산합니다. TSDF와 달리 먼 거리도 잘라내지 않습니다.

ESDF vs TSDF

측면	TSDF	ESDF
거리 범위	Truncation 범위 내만 정확	전체 공간에서 정확
표면 근처	정밀	정밀
표면에서 먼 곳	"최대값"으로 단순화	정확한 거리값 유지
기울기 정보	표면 근처에서만 유효	전체 공간에서 유효

ESDF의 핵심 장점

연속적인 기울기 정보: ESDF는 전체 공간에서 기울기가 유효하므로 최적화 기반 경로 계획에 적합합니다.

\nabla \text{ESDF}(x, y, z) = \text{장애물에서 멀어지는 방향}

활용 사례:

충돌 회피 경로 계획
연속 기울기 기반 궤적 최적화
로봇 이동 중 안전 거리 계산

TSDF vs ESDF: 언제 무엇을 사용할까?

용도	권장 방식	이유
표면 재구성	TSDF	표면 근처만 필요, 노이즈 제거 효과
3D 스캔/매핑	TSDF	효율적 저장, 점진적 업데이트
경로 계획	ESDF	전체 공간의 기울기 필요
충돌 회피	ESDF	어디서든 안전 거리 확인 가능
Sim-to-Real	TSDF → ESDF	표면 재구성 후 경로 계획

핵심 정리

Voxel은 3D 공간의 픽셀로, 각 위치에 물리적 속성을 저장하는 데이터 컨테이너입니다. Point Cloud와 달리 빈 공간 정보도 표현할 수 있습니다.
Occupancy Grid는 점유 여부만 저장하므로 "얼마나 가까운가?"와 "기울기"를 알 수 없습니다.
SDF는 각 Voxel에 가장 가까운 장애물까지의 거리와 부호를 저장합니다. 양수는 외부, 음수는 내부를 의미합니다.
TSDF는 표면 근처만 정밀하게 저장하여 노이즈를 제거하고 표면 재구성에 적합합니다.
ESDF는 전체 공간의 거리를 저장하여 연속적인 기울기 정보를 제공하므로 경로 계획과 충돌 회피에 적합합니다.

로봇이 3D 환경을 안전하게 탐색하려면 단순한 점유 정보가 아닌, 거리 정보와 기울기가 필요합니다. SDF 계열 기술은 이 요구사항을 효율적으로 해결합니다.

로봇이 3D 공간을 이해하는 방법: Voxel과 SDF

Voxel: 3D 공간의 데이터 컨테이너​

Point Cloud vs Voxel​

Occupancy Grid Map​

Occupancy Grid의 한계​

SDF: Signed Distance Fields​

SDF의 구성 요소​

SDF가 해결하는 문제​

TSDF: Truncated SDF​

TSDF의 특징​

TSDF의 장점​

TSDF 활용 사례​

ESDF: Euclidean SDF​

ESDF vs TSDF​

ESDF의 핵심 장점​

TSDF vs ESDF: 언제 무엇을 사용할까?​

핵심 정리​