Touch Probe와 Kabsch 알고리즘을 활용한 정밀 로봇 칼리브레이션

시뮬레이션에서 계획한 경로가 현실 로봇에서 0.5mm 이내로 동작하게 만드는 방법. Vision 기반 방식의 한계를 넘어 Touch Probe와 Kabsch 알고리즘으로 Sim-to-Real Gap을 극복한 실전 사례를 공유합니다.

Sim-to-Real Gap: 디지털 트윈의 가장 큰 장벽

많은 제조 현장에서 디지털 트윈(Digital Twin) 도입을 시도합니다. 하지만 대부분은 "화면에 실제 로봇과 똑같이 생긴 3D 모델을 띄우는 것"에서 멈춥니다.

진정한 디지털 트윈은 다릅니다. 가상 공간의 시뮬레이션 결과가 현실의 물리적 동작과 일치해야 완성됩니다.

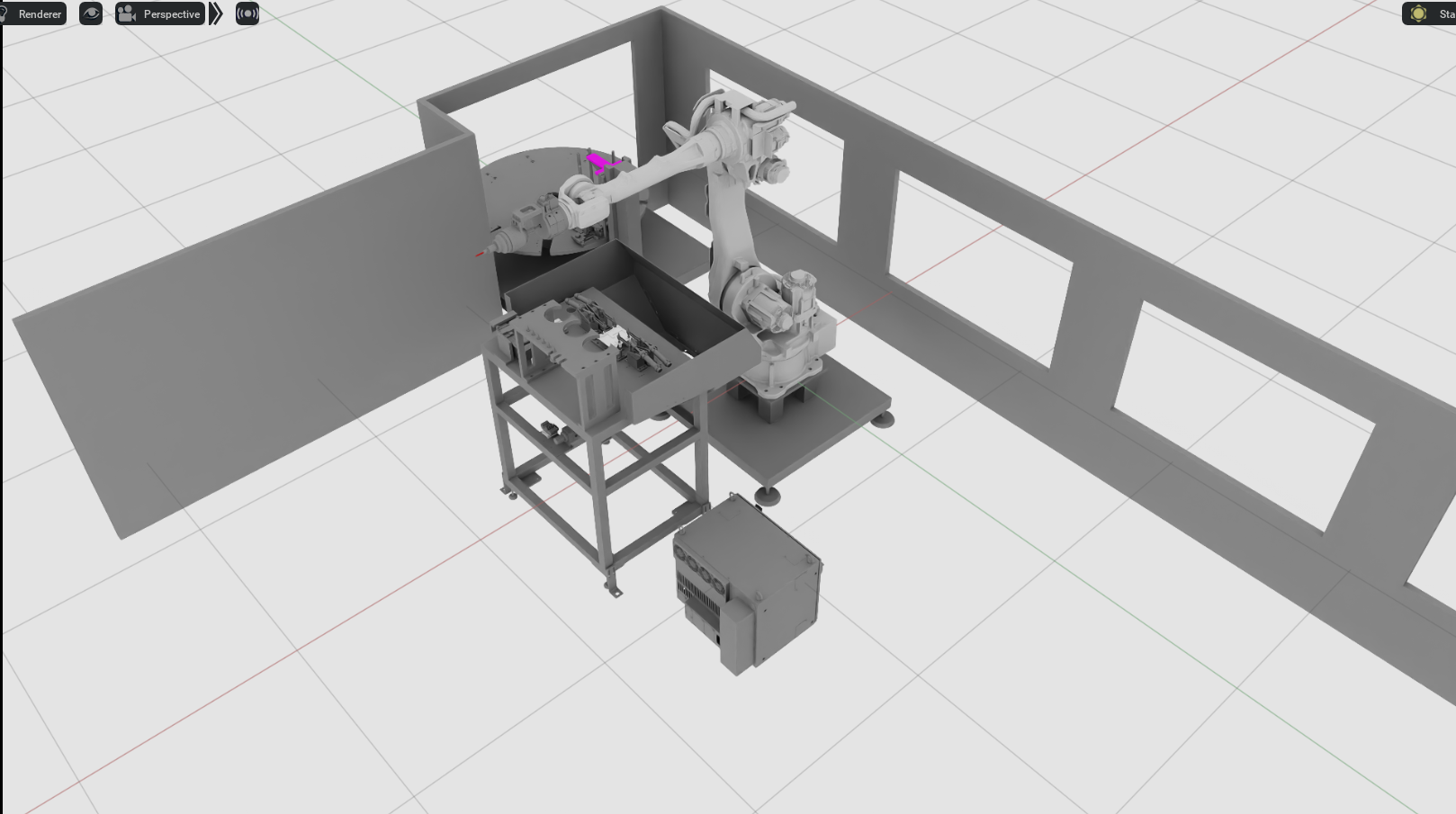
[위] 제공받은 공장 환경의 CAD 파일, [아래] CAD로부터 생성한 시뮬레이션 환경

문제는 시뮬레이션과 현실 사이의 간극입니다.

시뮬레이션의 이상적 가정

• 로봇은 완벽한 강체(Rigid Body)
• 관절은 완벽한 회전축을 가짐
• 마찰이나 백래시(Backlash) 없음

현실의 불완전함

현실 로봇은 수많은 오차 요인을 가집니다:

기구학적 오차(Kinematic Errors)

• 가공 공차로 인한 실제 링크 길이와 CAD 모델 간의 미세한 차이
• 조립 불량으로 인한 관절 축 오정렬

비기구학적 오차(Non-Kinematic Errors)

• 중력으로 인한 로봇 팔의 처짐
• 기어 유격(Gear Backlash)
• 온도에 따른 금속의 팽창/수축

이 오차들이 로봇, 엔드 이펙터, 작업 환경의 모든 요소에 적용되고 누적됩니다.

로봇 칼리브레이션은 단순한 좌표 설정이 아닙니다. 현실의 불완전한 물리적 파라미터를 측정하여 가상 모델에 보정하는 기술입니다.

칼리브레이션 방법론 비교

산업 현장에서 사용되는 칼리브레이션 방법은 정밀도 요구사항과 비용에 따라 세 가지로 나뉩니다.

1. 수동 티칭 (Manual Teaching)

가장 직관적인 방법입니다. 작업자가 티칭 펜던트로 로봇 TCP(Tool Center Point)를 물체에 직접 접촉시켜 좌표계를 계산합니다.

한계점:

• 작업자 숙련도에 따른 결과 편차 (Human Error)
• 공정 변경 시 매번 재티칭 필요
• 일관성 확보 어려움

2. 비전 센서 기반 (Hand-Eye Calibration)

카메라로 체커보드나 마커를 인식하여 $AX = ZB$ 형태의 행렬 연산으로 좌표를 변환합니다.

장점: 자동화 가능, 비접촉식, 빠른 측정

한계점:

• 렌즈 왜곡(Distortion)으로 인한 추가 오차
• 조명 환경에 민감
• 거리에 따른 분해능 저하

3. 정밀 계측 장비 (Laser Tracker 등)

레이저 트래커로 1mm 이하의 정밀도를 달성할 수 있습니다.

한계점:

• 장비 도입 비용 수천만 원 이상
• 설치 환경 제약

방법	장점	단점	정밀도
수동 티칭	직관적, 추가 장비 불필요	Human Error, 재현성 낮음	1~3mm
비전 센서	자동화 가능, 비접촉식	조명/왜곡 변수	0.5~2mm
레이저 트래커	매우 높은 정밀도	고가, 설치 제약	＜0.1mm

초기 시도: ArUco 마커의 한계

우리의 첫 접근은 가장 범용적인 ArUco 마커 기반 방식이었습니다.

카메라로 마커 코너를 검출하고, PnP(Perspective-n-Point) 알고리즘으로 3차원 위치와 자세를 추정합니다. 기존 Pick & Place 태스크에서는 효율적으로 동작했습니다.

하지만 이번 프로젝트는 0.5mm 이하의 초정밀도를 요구했습니다.

비전 기반 방식의 구조적 한계

1. 검출값 떨림(Jittering)

조명의 미세한 변화, 센서 노이즈로 측정값이 계속 흔들립니다. 통계적으로 평균을 내도 서브밀리미터 정밀도는 어렵습니다.

2. 거리와 해상도의 반비례

로봇의 넓은 작업 반경을 커버하려면 카메라를 멀리 배치해야 합니다. 거리가 멀어질수록 픽셀당 실제 거리가 증가하여 분해능이 급격히 떨어집니다.

ArUco 방식으로 1mm 내외의 정밀도는 확보했지만, 0.5mm 이하는 구조적으로 불가능했습니다.

새로운 접근: Touch Probe + Kabsch 알고리즘

Touch Probe를 선택한 이유

고가의 레이저 트래커 도입은 비현실적이었습니다. 우리는 "가장 원초적인 방식이 가장 정확할 수 있다"는 점에 주목했습니다.

Touch Probe의 강점:

1. 물리적 접촉 기반 측정 - 조명, 렌즈 왜곡 영향 없음
2. 로봇 반복 정밀도(Repeatability) 활용 - 산업용 로봇의 반복 정밀도는 0.02~0.05mm 수준
3. 자동화된 탐색(Automated Probing) - Human Error 배제
4. 비용 효율성 - 레이저 트래커 대비 1/10 이하 비용

Renishaw의 Touch Trigger Probe는 0.25μm 반복 정밀도를 제공합니다. 로봇의 반복 정밀도와 결합하면 서브밀리미터 칼리브레이션이 가능해집니다.

Kabsch 알고리즘: 최적 회전 변환 도출

Touch Probe로 측정한 점들과 시뮬레이션 상의 점들 사이의 최적 변환 행렬을 구해야 합니다.

Kabsch 알고리즘은 두 점군(Point Cloud) 사이의 RMSD(Root Mean Square Deviation)를 최소화하는 회전 행렬과 이동 벡터를 계산합니다.

최적화 문제 정의

두 점군 $P = \{\mathbf{p}_1, \mathbf{p}_2, ..., \mathbf{p}_N\}$와 $Q = \{\mathbf{q}_1, \mathbf{q}_2, ..., \mathbf{q}_N\}$가 주어졌을 때:

$$\min_{R, \mathbf{t}} \frac{1}{2} \sum_{i=1}^{N} d(\mathbf{q}_i, R\mathbf{p}_i + \mathbf{t})^2$$

여기서 $R$은 회전 행렬, $\mathbf{t}$는 이동 벡터입니다.

Step 1: 중심화 (Centroid Calculation)

두 점군의 무게 중심(Centroid)을 계산합니다:

$$\bar{\mathbf{p}} = \frac{1}{N} \sum_{i=1}^{N} \mathbf{p}_i, \quad \bar{\mathbf{q}} = \frac{1}{N} \sum_{i=1}^{N} \mathbf{q}_i$$

중심화된 점군을 생성합니다:

$$\mathbf{p}'_i = \mathbf{p}_i - \bar{\mathbf{p}}, \quad \mathbf{q}'_i = \mathbf{q}_i - \bar{\mathbf{q}}$$

시뮬레이션 위치(Q_centered)와 실제 환경 위치(P_centered)의 중심화된 점군

Step 2: 공분산 행렬 계산 (Covariance Matrix)

두 점군 사이의 상관관계를 나타내는 $3 \times 3$ 공분산 행렬 $H$를 계산합니다:

$$H = P'^T Q'$$

여기서 $P'$와 $Q'$는 각각 중심화된 점들을 행(row)으로 갖는 $N \times 3$ 행렬입니다.

Step 3: 특이값 분해 (SVD)

공분산 행렬 $H$를 SVD로 분해합니다:

$$H = U \Sigma V^T$$

• $U$: $3 \times 3$ 직교 행렬
• $\Sigma$: 특이값을 담은 대각 행렬
• $V^T$: $3 \times 3$ 직교 행렬

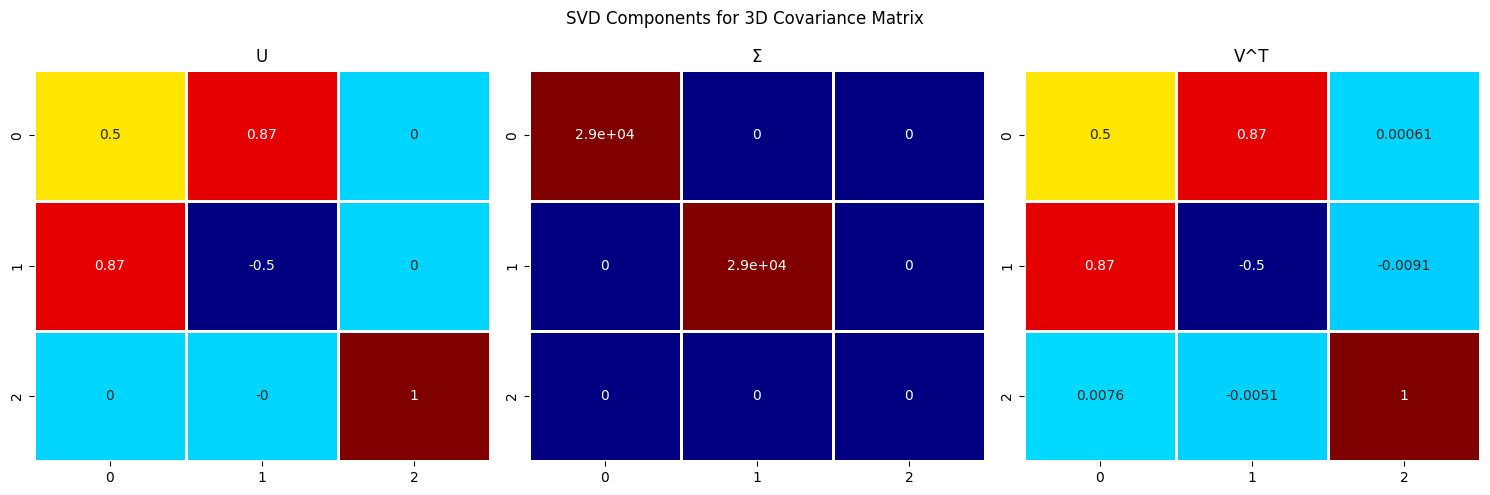
실제 계산에 사용된 SVD 분해 결과

Step 4: 최적 회전 행렬 도출

SVD 결과로부터 최적 회전 행렬 $R$을 계산합니다:

$$R = V U^T$$

반사(Reflection) 처리:

$\det(VU^T) = -1$인 경우, 회전이 아닌 반사가 발생합니다. 이를 보정하기 위해:

$$R = V \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & d \end{bmatrix} U^T, \quad d = \text{sign}(\det(VU^T))$$

Step 5: 이동 벡터 계산

최적 이동 벡터 $\mathbf{t}$는 중심점들로부터 계산합니다:

$$\mathbf{t} = \bar{\mathbf{q}} - R\bar{\mathbf{p}}$$

최종 변환 행렬

회전 $R$과 이동 $\mathbf{t}$를 결합한 $4 \times 4$ 동차 변환 행렬:

$$T_{calib} = \begin{bmatrix} R & \mathbf{t} \\ \mathbf{0}^T & 1 \end{bmatrix}$$

수학적 최적성 보장

Kabsch 알고리즘은 RMSD를 최소화하는 해를 수학적으로 보장합니다:

$$\text{RMSD} = \sqrt{\frac{1}{N} \sum_{i=1}^{N} d(\mathbf{q}_i, R\mathbf{p}_i + \mathbf{t})^2}$$

여기서 $d(\cdot, \cdot)$는 유클리드 거리(Euclidean distance)입니다.

SVD 기반 풀이가 닫힌 형태(Closed-form)의 최적해를 제공하므로, 반복적 최적화 대비 계산이 빠르고 수렴 문제가 없습니다.

실제 적용 결과

계산된 회전 변환

우리 프로젝트에서 Kabsch 알고리즘으로 계산된 오일러 각:

축	라디안	각도
Roll	0.005054	0.289582°
Pitch	0.007563	0.433337°
Yaw	-0.001171	-0.067092°

매우 작은 회전 오차지만, 로봇 팔 끝단에서는 수 밀리미터의 위치 오차로 증폭됩니다.

변환 적용 결과

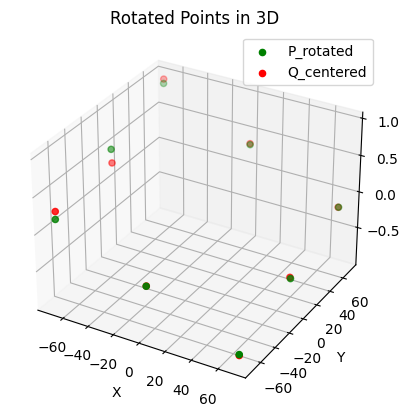
알고리즘을 통해 계산된 회전 변환 적용 후 정렬된 점군(P_rotated)

Sim-to-Real Gap 극복

보정 행렬 $T_{calib}$를 로봇 제어기에 실시간으로 피드백하여, 가상 시뮬레이션에서 생성한 경로를 현실의 틀어진 환경에 정확히 매핑했습니다.

결과: Vision 기반으로 불가능했던 0.5mm 이내 정밀도 달성

구현 코드 예시

import numpy as np
from scipy.spatial.transform import Rotation

def kabsch_algorithm(P: np.ndarray, Q: np.ndarray) -> tuple[np.ndarray, np.ndarray]:
    """
    Kabsch 알고리즘으로 최적 회전 행렬과 이동 벡터 계산

    Args:
        P: 소스 점군 (N x 3)
        Q: 타겟 점군 (N x 3)

    Returns:
        R: 최적 회전 행렬 (3 x 3)
        t: 최적 이동 벡터 (3,)
    """
    # Step 1: 중심화
    centroid_P = np.mean(P, axis=0)
    centroid_Q = np.mean(Q, axis=0)

    P_centered = P - centroid_P
    Q_centered = Q - centroid_Q

    # Step 2: 공분산 행렬
    H = P_centered.T @ Q_centered

    # Step 3: SVD
    U, S, Vt = np.linalg.svd(H)

    # Step 4: 회전 행렬 (반사 보정 포함)
    d = np.sign(np.linalg.det(Vt.T @ U.T))
    R = Vt.T @ np.diag([1, 1, d]) @ U.T

    # Step 5: 이동 벡터
    t = centroid_Q - R @ centroid_P

    return R, t


def compute_rmsd(P: np.ndarray, Q: np.ndarray, R: np.ndarray, t: np.ndarray) -> float:
    """변환 적용 후 RMSD 계산"""
    P_transformed = (R @ P.T).T + t
    return np.sqrt(np.mean(np.sum((Q - P_transformed) ** 2, axis=1)))


# 사용 예시
if __name__ == "__main__":
    # 시뮬레이션 점군 (Touch Probe 측정 위치)
    P_sim = np.array([
        [100.0, 0.0, 50.0],
        [200.0, 0.0, 50.0],
        [150.0, 100.0, 50.0],
        # ... 추가 측정점
    ])

    # 실제 환경 점군 (Touch Probe 실측 위치)
    P_real = np.array([
        [100.12, 0.45, 49.87],
        [200.15, 0.52, 49.91],
        [150.08, 100.38, 49.82],
        # ... 추가 측정점
    ])

    R, t = kabsch_algorithm(P_real, P_sim)
    rmsd = compute_rmsd(P_real, P_sim, R, t)

    # 오일러 각 추출
    euler = Rotation.from_matrix(R).as_euler('xyz', degrees=True)

    print(f"RMSD: {rmsd:.4f} mm")
    print(f"Roll: {euler[0]:.4f}°, Pitch: {euler[1]:.4f}°, Yaw: {euler[2]:.4f}°")
    print(f"Translation: {t}")

핵심 정리

1. Sim-to-Real Gap은 디지털 트윈 성공의 가장 큰 장벽입니다. 기구학적/비기구학적 오차가 누적되어 현실과 시뮬레이션 사이에 간극이 발생합니다.

2. 비전 기반 칼리브레이션은 편리하지만, 서브밀리미터 정밀도가 필요한 공정에서는 구조적 한계가 있습니다.

3. Touch Probe는 물리적 접촉 기반으로 조명/왜곡 영향이 없고, 로봇의 반복 정밀도를 활용한 자동화가 가능합니다.

4. Kabsch 알고리즘은 SVD 기반으로 RMSD를 최소화하는 최적 변환 행렬을 수학적으로 보장합니다.

5. 두 기술의 결합으로 0.5mm 이하의 Sim-to-Real 칼리브레이션을 달성할 수 있습니다.

정밀한 칼리브레이션은 화려한 장비가 아니라, 적절한 알고리즘과 측정 원리의 선택에서 시작합니다.